als.c File Reference

Implementation of subroutines handling sets of inidices (union, intersection, merge, cardinal ...) More...

Go to the source code of this file.

Functions
int	card (int *A, int nA)
void	merge (int *A, int nA, int *B)
int	card_or (int *A1, int n1, int *A2, int n2)
int	card_and (int *A1, int n1, int *A2, int n2)
int	set_or (int *A1, int n1, int *A2, int n2, int *A1orA2)
int	set_and (int *A1, int n1, int *A2, int n2, int *A1andA2)
int	map_and (int *A1, int n1, int *A2, int n2, int *mapA1andA2)
	Compute map A1 and A2 / A1. More...
void	subset2map (int *A, int nA, int *subA, int nsubA)

Detailed Description

Implementation of subroutines handling sets of inidices (union, intersection, merge, cardinal ...)

Note

Copyright (c) 2010-2012 APC CNRS Université Paris Diderot. This program is free software; you can redistribute it and/or modify it under the terms of the GNU Lesser General Public License as published by the Free Software Foundation; either version 3 of the License, or (at your option) any later version. This program is distributed in the hope that it will be useful, but WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the GNU Lesser General Public License for more details. You should have received a copy of the GNU General Public License along with this program; if not, see http://www.gnu.org/licenses/lgpl.html

For more information about ANR MIDAS'09 project see http://www.apc.univ-paris7.fr/APC_CS/Recherche/Adamis/MIDAS09/index.html

ACKNOWLEDGMENT: This work has been supported in part by the French National Research Agency (ANR) through COSINUS program (project MIDAS no. ANR-09-COSI-009).

Author

Pierre Cargemel

Date

April 2012

Definition in file als.c.

Function Documentation

card()

int card	(	int *	A,
		int	nA
	)

Compute cardinal(A) Perform a loop onto elements of a set, counting different elements. The array should be in ascending order with possible redundancy.

Parameters

n	number of elemnets in A
A	set of indices

Returns

number of elements in A

Definition at line 29 of file als.c.

merge()

void merge	(	int *	A,
		int	nA,
		int *	B
	)

Merge redundant elements. Fill a new array containing elements of A, merging redundant elements. The array A should be in ascending order with possible redundancy. The array B has to be allocated.

Parameters

nA	number of elemnets in A
A	set of indices
B	output array

Returns

void

Definition at line 51 of file als.c.

card_or()

int card_or	(	int *	A1,
		int	n1,
		int *	A2,
		int	n2
	)

Compute 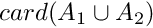A1 and A2 should be two ascending ordered monotmony sets. of size n1 and n2.

Parameters

n1	number of elemnets in A1
A1	set of indices
n2	number of elemnets in A2
A2	set of indices

Returns

size of the union

Definition at line 72 of file als.c.

card_and()

int card_and	(	int *	A1,
		int	n1,
		int *	A2,
		int	n2
	)

Compute 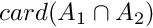A1 and A2 should be two ascending ordered monotony sets, of size n1 and n2.

Parameters

n1	number of elemnets in A1
A1	set of indices
n2	number of elemnets in A2
A2	set of indices

Returns

size of the intersection

Definition at line 111 of file als.c.

set_or()

int set_or	(	int *	A1,
		int	n1,
		int *	A2,
		int	n2,
		int *	A1orA2
	)

Compute 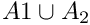A1 and A2 should be two ascending ordered sets. It requires the sizes of these two sets, n1 and n2. A1andA2 has to be previouly allocated.

Parameters

n1	number of elemnets in A1
A1	set of indices
n2	number of elemnets in A2
A2	set of indices
address	to the set A1orA2

Returns

number of elements in A1orA2

Definition at line 138 of file als.c.

set_and()

int set_and	(	int *	A1,
		int	n1,
		int *	A2,
		int	n2,
		int *	A1andA2
	)

Compute 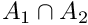A1 and A2 should be two monotony sets in ascending order. It requires the sizes of these two sets, n1 and n2. A1andA2 has to be previously allocated.

Parameters

n1	number of elemnets in A1
A1	set of indices
n2	number of elemnets in A2
A2	set of indices
address	to the set A1andA2

Returns

number of elements in A1andA2

Definition at line 186 of file als.c.

map_and()

int map_and	(	int *	A1,
		int	n1,
		int *	A2,
		int	n2,
		int *	mapA1andA2
	)

Compute map A1 and A2 / A1.

Parameters

n1	number of elemnets in A1
A1	set of indices
n2	number of elemnets in A2
A2	set of indices
address	to the set A1andA2

Returns

number of elements in A1andA2

Definition at line 210 of file als.c.

subset2map()

void subset2map	(	int *	A,
		int	nA,
		int *	subA,
		int	nsubA
	)

Transform a subset into a mapper array Parse a subset and replace element by his index in the larger set. A and subA should be two monotony sets in ascending ordered. subA has to belong to A.

Parameters

A	a set of indices(monotony)
nA	number of elemnets in A
subA	a subset of A(monotony)
nsubA	number of elemnets in A

Returns

void

Definition at line 237 of file als.c.